Projekt (Matlab) - rozwinięcie funkcji w szereg
Skrypt z programowania w środowisku Matlab:
Temat zadania:
Przygotować skrypt tablicujący funkcję oraz jej rozwinięcie w szereg w podanym przedziale.
Skrypt powinien przyjmować następujące dane wejściowe:
Przedział określony przez parametry A i B podzielić na N odcinków uzyskując w ten sposób N+1 punktów. Dla każdego punktu obliczyć:
Przygotować skrypt tablicujący funkcję oraz jej rozwinięcie w szereg w podanym przedziale.
Skrypt powinien przyjmować następujące dane wejściowe:
- A - początek przedziału,
- B - koniec przedziału,
- N - liczba podziałów przedziału,
- LW - liczba wyrazów szeregu (ocena 3.0) lub ε - dokładność (ocena > 3.0).
Przedział określony przez parametry A i B podzielić na N odcinków uzyskując w ten sposób N+1 punktów. Dla każdego punktu obliczyć:
- wartość funkcji,
- wartość rozwinięcia w szereg - korzystając z LW lub ε,
- błąd względny,
- błąd bezwzględny
Zasady oceniania projektu:
Przygotowany projekt należy wysłać najpóźniej dzień przed terminem zajęć zaliczeniowych. Oceniane będą przygotowanie projektu oraz odpowiedzi na pytania zadane podczas oddawania projektu. W przypadku braku odpowiedzi na wszystkie pytania, projekt nie będzie zaliczony.
Ocena 3.0 - działający poprawnie program, wykorzystujący stałą liczbę wyrazów (LW) do obliczenia sumy szeregu.
Ocena 4.0 - działający poprawnie program, kontrolujący dokładność (ε) obliczeń sumy szeregu i sprawdzający poprawność wprowadzonych danych.
Ocena 5.0 - działający poprawnie program, kontrolujący dokładność (ε) obliczeń sumy szeregu i sprawdzający poprawność wprowadzonych danych oraz prezentujący wyniki w formie graficznej (wykresy funkcji i jej przybliżenia oraz wykres błędu).
Przygotowany projekt należy wysłać najpóźniej dzień przed terminem zajęć zaliczeniowych. Oceniane będą przygotowanie projektu oraz odpowiedzi na pytania zadane podczas oddawania projektu. W przypadku braku odpowiedzi na wszystkie pytania, projekt nie będzie zaliczony.
Ocena 3.0 - działający poprawnie program, wykorzystujący stałą liczbę wyrazów (LW) do obliczenia sumy szeregu.
Ocena 4.0 - działający poprawnie program, kontrolujący dokładność (ε) obliczeń sumy szeregu i sprawdzający poprawność wprowadzonych danych.
Ocena 5.0 - działający poprawnie program, kontrolujący dokładność (ε) obliczeń sumy szeregu i sprawdzający poprawność wprowadzonych danych oraz prezentujący wyniki w formie graficznej (wykresy funkcji i jej przybliżenia oraz wykres błędu).
Przykładowe wyniki z programu:
Dane wejściowe:
A = -0.2
B = 0.2
N = 20
ε = 1e-8
Wyniki:
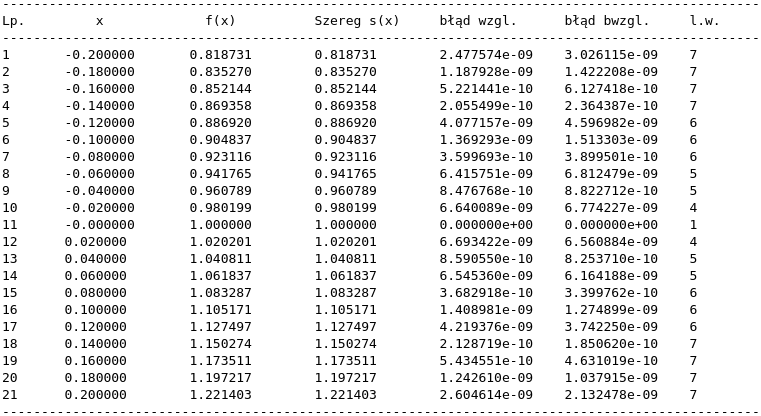
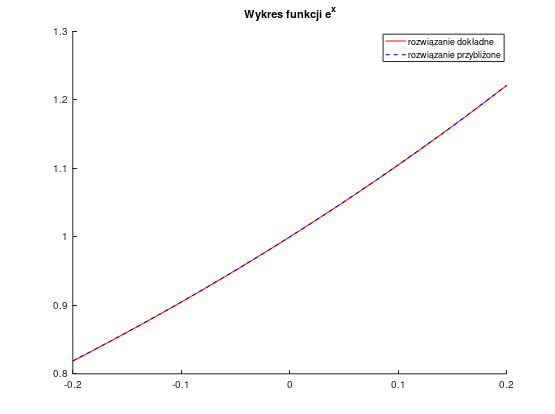
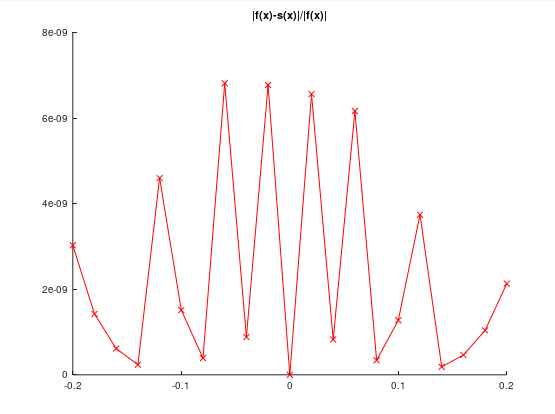
Dane wejściowe:
A = -0.1
B = 0.1
N = 20
ε = 1e-1
Wyniki:
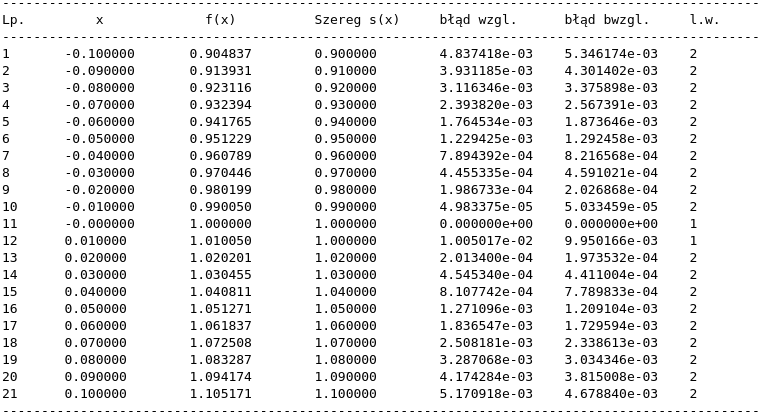
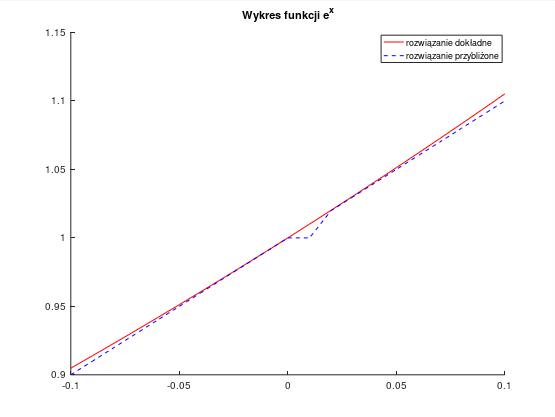
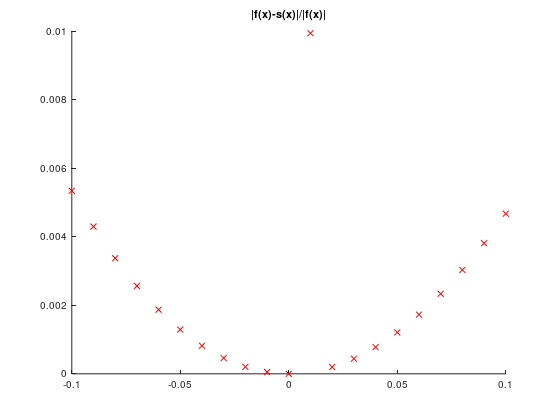
Dane wejściowe:
A = -0.2
B = 0.2
N = 20
ε = 1e-8
Wyniki:



Dane wejściowe:
A = -0.1
B = 0.1
N = 20
ε = 1e-1
Wyniki:



Przydatne instrukcje/algorytmy:
Wyświetlanie sformatowanego tekstu:
Wczytywanie danych z klawiatury:
Wyświetlanie wykresów:
Tablicowanie funkcji:
Rozdział 4, sekcja 4.1: Tablicowanie funkcji
Obliczanie szeregów:
Rozdział 5, sekcja 5.3: Suma nieskończona
Rozdział 5, sekcja 5.7: Szeregi funkcyjne
Wyświetlanie sformatowanego tekstu:
fprintf('%g \t %f \t %e \n', nr, x, fun')
- %g - wyświetlenie liczby całkowitej (za %g zostanie wstawiona wartość zmiennej nr),
- \t - zapisanie znaku tabulacji,
- %f - wyświetlenie liczby zmiennoprzecinkowej (za %f zostanie wstawiona wartość zmiennej x),
- %e - wyświetlenie liczby w notacji naukowej (za %e zostanie wstawiona wartość zmiennej fun),
- \n - zapisanie znaku nowej linii.
Wczytywanie danych z klawiatury:
N = input('Podaj liczbę podziałów N');
Wyświetlanie wykresów:
x = 0:0.1:2;
y = x.^2;
z = x.^3;
figure();
plot(x, y);
hold on;
plot(x, z);
title('Wykres dwóch funkcji');
legend('x^2', 'x^3');
Tablicowanie funkcji:
Rozdział 4, sekcja 4.1: Tablicowanie funkcji
Obliczanie szeregów:
Rozdział 5, sekcja 5.3: Suma nieskończona
Rozdział 5, sekcja 5.7: Szeregi funkcyjne